EL MÉTODO EXHAUSTIVO
INTRODUCCIÓN
Los problemas más controvertibles y de mayor importancia en la construcción de una teoría de la medida, son aquellos en los cuales aparecen procesos infinitos. Las magnitudes inconmensurables son un claro ejemplo de ello, pues involucran la prolongación ilimitada del proceso de búsqueda de una medida común. También sucede algo similar en el cálculo de algunas áreas y volúmenes como lo mostraría Arquímedes.
Algunos matemáticos griegos “hallaron” la salida conceptual a estas dificultades a través de las teorías atomistas de Leucipo y Democrito(460-370 a. C.). Muchos de los conceptos sobre infinitesimales en matemáticas, así como su aplicación al calculo de cuadraturas, se basa en las ideas atomistas, especialmente los esfuerzos por caracterizar las magnitudes continuas a partir de un conjunto de partículas infinitamente pequeñas(átomos).
Sin embargo, la aparición de contradicciones como las paradojas de Zenón, demostrarían que esta salida era muy endeble. Zenón argumentaba contra los atomistas mostrando que era imposible una teoría rigurosa de la demostración en la cual se diera cuenta de los procesos infinitos, apoyándose en las consideraciones atomistas ingenuas.
Es cuando aparece, el método exhaustivo! Surge como método de solución a este problema, es decir como respuesta a las paradojas surgidas en el tratamiento de los procesos infinitos.
Para llevar a cabo la cuadratura o cubatura de una figura, Eudoxo, Euclides y Arquímedes debían encontrar su razón con otra figura previamente conocida. Es por ello por lo que, como se ha visto, los griegos desarrollaron una sofisticada teoría de magnitudes y proporciones, sobre todo por parte de Eudoxo.
Eudoxo de Cnido es uno de los matemáticos más importantes de la Academia platónica, que al Introducir la idea de "tan pequeño como se quiera", antecedente de nuestro proceso de "paso al límite", encuentra una escapatoria a los problemas planteados por el infinito y lo inconmensurable, mediante un recurso genial que desarrolla en tres pasos:

1. Una definición: igualdad de razones, Euclides, Definición V.5.
2. Un axioma: axioma de Eudoxo-Arquímedes o axioma de continuidad, Euclides, Definición V.4.
3. Un método: el Método de Exhaución, Euclides, Proposición X.1.
Como lo inexpresable era la razón entre dos cantidades inconmensurables, Eudoxo elimina la dificultad definiendo no la razón misma, sino la igualdad de razones de la siguiente forma
Definición V.5 de Los Elementos de Euclides:
"Se dice que una primera magnitud guarda la misma razón con una segunda magnitud,que una tercera magnitud con una cuarta magnitud, cuando cualesquiera equimúltiplos de la primera y la tercera exceden a la par, sean iguales a la par o sean inferiores a la par, que cualesquiera equimúltiplos de la segunda y la cuarta, respectivamente y tomados en el orden correspondiente".
Es decir:
Si a,b son dos magnitudes geométricas del mismo tipo y c,d son también del mismo tipo (aunque no necesariamente del mismo tipo que a y b), Eudoxo define que las razones:
a/b y c/d son proporcionales: a/b = c/d,
cuando para cualquier par de enteros positivos n y m, se tiene:
na>mb y nc>md ó na = mb y nc = md, ó na<mb y nc<md
Dado que el problema de la época era intentar hallar el área de figuras no rectilíneas, entre ellas el circulo, se buscaba la forma de encontrar dicho tipo de áreas; al respecto Eudoxo, propone que lo mejor que se puede hacer(para el caso del circulo), es inscribir en la circunferencia correspondiente figuras rectilíneas que tuviesen cada vez un mayor número de lados, y proceder a calcular sus áreas indefinidamente. De este modo, la superficie de los polígonos inscritos se aproximaran cada vez más a la superficie de la figura curvilínea.
Pero una estricta definición de limite era desconocida, de modo que no podían dar a este razonamiento de las aproximaciones una argumentación lógica: ¿ Hasta dónde era posible aproximarse?
Puesto que el polígono inscrito podía aproximarse al circulo sin llegar nunca a cubrirlo completamente, ¿ era entonces imposible llegar a determinar exactamente el área de un circulo cualquiera?
El axioma que permitiría a Eudoxo solucionar este problema, es el expuesto, como la primera proposición de el libro X de los Elementos de Euclides, la cual Euclides demuestra:
Proposición X.1: (Elementos) Dadas dos magnitudes desiguales, si de la mayor se resta una magnitud mayor que su mitad y de lo que queda otra magnitud mayor que su mitad y se repite continuamente este proceso, quedara una magnitud menor que las magnitudes dadas.
La metodología Arquimediana
La mayor parte de los trabajos de Arquímedes se refieren a la determinación de áreas de superficies curvas y volúmenes de sólidos, que se obtienen a través de la comparación. Su técnica demostrativa más poderosa es la combinación de un procedimiento de demostración por reducción al absurdo con el llamado método de exhaución.

Arquimedes retoma el metodo exhaustivo planteado por Eudoxo, de la siguiente manera:
La esencia matemática de este método consiste en la sucesión de las siguientes operaciones o pasos, tomando como referencia una figura curvilínea R:
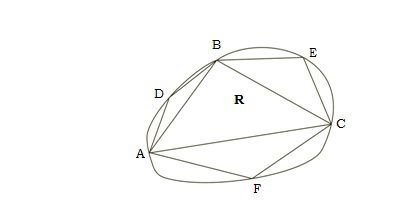
1. Se inscribe (circunscribe) una sucesión de figuras rectilíneas A1, A2,. . .An,. . . cuyas áreas crecen monótonamente. En este caso: A1 = ABC, A2 = ADBECF,. . ., etc.
2. Las figuras se escogen de tal suerte que la sucesión a(R) – α(A1), a(R) – α(A2), . . ., α(R) – α(An), . . . cumpla con las hipótesis de X.1. de los Elementos.
3. Con ayuda de consideraciones teóricas, se presume el “límite” en la sucesión de las figuras inscritas, el cual se designa por a(A).
En general, el procedimiento para la obtención del límite no se especifica; se recurre a la intuición se supone que se ha recurrido al proceso prueba error, intentando visualizar una ley de formación en la suma, de todas las áreas de los polígonos inscritos.
4. Se demuestra que el “limite a(A)” , es igual al área buscada a(R). Esta demostración se realiza por reducción al absurdo, veamos:
a. Se supone a(R) > a(A) , de lo cual a(R) – a(A)> 0, y por lo tanto, por el principio de Eudoxo, existe n tal que a(R) – a(An) < a(R) – a(A); esto significa que a(An) >a(A) , lo cual es imposible.
b. Se supone a(R) < a(A) , de lo cual a(A) – a(R) > 0, y por lo tanto, dado que la sucesión {An} tiene por límite A, se tiene que existe n tal que, a(A) – a(An)< a(A) - a(R) y de aquí se deduce que a(An)>a(R) lo cual es imposible.
En términos generales, es una aproximación entre figuras geométricas conocidas, inscritas y circunscritas, sobre otra por conocer, de manera que la diferencia entre unas y otras sea tan pequeña que se consideren equivalentes. En tal procedimiento interviene un razonamiento lógico que garantiza la verdad de la aseveraciones geométricas: la reducción al absurdo. Así, la negación de la equivalencia entre las áreas ocasiona una contradicción lógica insoluble, lo cual nos obliga, en aras de mantener el procedimiento lógicamente coherente, a aceptarla como verdadera.
ARQUIMEDES Y LA CUADRATURA DEL CIRCULO
En su texto Medida del círculo, Arquímedes presenta tres proposiciones en las cuales expone sus avances en la resolución del problema clásico de la cuadratura del círculo. En la primera proposición demuestra que todo círculo es equivalente a un triangulo rectángulo cuyos catetos corresponden al radio y a la longitud de la circunferencia. Ello significa que la cuadratura del círculo es posible a condición de que se pueda calcular la longitud de la circunferencia. Para ello Arquímedes se apoya en el hecho que la razón entre la longitud de la circunferencia y el radio es constante.
EL METODO EXHAUSTIVO APLICADO AL CÍRCULO
Un resultado usado por Arquímedes, es basado en el proceso demostrativo que usa Euclides, para su proposición XII. 2
Euclides demuestra que el área de un círculo se puede agotar por medio de polígonos inscritos; esto es, dado un círculo C y un numero ε > 0, existe un polígono P inscrito en C, tal que, a(C) – a(P) < ε, donde a(C) corresponde al área del círculo C y a(P) al área del polígono P.
REFERENTES BIBLIOGRAFICOS:
Luis Cornelio Recalde, Arquimedes y el problema de las cuadraturas. Universidad del Valle.
José Luis Montesinos Sirera, ARQUÍMEDES Y LA MEDIDA DEL CIRCULO.(Pág. 41)
Ángel Molina, Universidad del Zulia; El método de investigación de Arquímedes de Siracusa : Intuición, mecánica y exhaución


